Infinitesimals - Do They Exist? Perhaps only in the
minds of
certain mathematicians. Nevertheless, they are a fascinating concept.
But first, a brief look at the history and structure of the real
numbers.
Today we think of this set as equivalent to the set of points
of
the real line - a sort of ruler extending endlessly in both directions
from the point corresponding to zero. To the ancient Greeks,
there were only points corresponding to rational
numbers
(ratios of whole numbers, e.g., 2/5) and between any two points on a
line there were only a finite number of such rational "points". When irrational
numbers
were discovered, they were deemed "incommensurable", meaning they could
not be expressed as such ratios and, in a sense, were non-measurable.
Nowadays, we think of the real numbers as composed of both rationals and irrationals, "filling up" the real line. Between any two real numbers, a and b, are both a rational and an irrational, and, therefore, and infinite number of each in the interval [a,b]. Whereas the rationals can be shown to be "countable" (a discrete scheme for counting them can be devised), the irrationals are known to be "uncountable" (no such scheme can, in principle, exist). A famous mathematician once compared the stars in the night sky to be like the rational numbers, and the blackness between them, the irrational numbers. Together they consitute the entirety of the numbers we use in the every-day world. In terms of familiar decimal representations, the rationals are all either terminating (e.g., 2/5 = .4) or non-terminating but repeating (e.g., 3/11 = .27272727. . .). Those decimal expansions that neither terminate nor repeat represent irrationals (e.g., π = 3.14159 . . .). Now, back to infinitesimals. Newton, in 1669, defines the moment of x to be an "infinitesimal" increase in the the value of a real number, x. It appears to be indivisible, and thus something of an enigma. Leibniz, in the late 1600s, speaks of monads, ultimate infinitesimal particles from which nature arises. He used this idea in his mathematics, alluding to what we now call the differential, dx, as being not 0 but smaller than any finite quantity. As mathematical sophistication increased during the next two centuries, the ideas of Cauchy, Weierstrass and others took hold, and monads and moments - in their original guise - faded away. In the Standard Analysis that derived from their work, all real numbers were either rational or irrational, and "infinitesimal" came to mean simply very, very small, but real. Then, in the early 1960s, Abraham Robinson and others demonstrated that there exists a kind of extension of the real number system that includes non-traditional "real" elements: infinitesimals, ε , where |ε| < r, for all positive real numbers, r. Robinson showed that all the rules of arithmetic and algebra apply to this new, enlarged system, which includes, as well, numbers that are infinite. I.e., numbers of the form ω, where for each such ω, |ω| > n for all standard integers n. The normal rules for inequalities hold, so that ∞+1 > ∞, and so on. It follows that 1/ω is an infinitesimal, and 1/ε is infinite (except that division by 0 is not allowed). Robinson resurrects the word monad (of x) to mean all real numbers infinitely close to x ; i.e., of the form x + ε . Other authors use pleasing terms like "mist" or "cloud" or "halo" to describe this concept. In the complex plane, infinitesimals may be of the form α + iβ , or <α,β>, where α and β are real infinitesimals. The "halo" or "complex monad" of a standard z becomes two dimensional:  (How
would you
picture it?)
There
have been
philosophical speculations about whether infinitesimals do actually
correspond to points on a line (or in the complex plane). A point is
dimensionless, so perhaps
there are "positions" for both standard and non-standard real numbers
on our ruler. After all, irrational
numbers
are never used in measurements by empirical scientists - all
measurements are ultimately rational. One simple arithmetic operation
involving the decimal forms of true irrational numbers would take an
infinite amount of time to complete - even on the hypothetically best
computers. It would take an eternity to even fully and completely
describe the decimal forms. So, are the irrationals as abstract and
strange as infinitesimals? Not quite, but there's more to them than one
normally thinks.There is an effective limit to the measurability of distances between points that are extremely close together. So, in a sense, there are "spaces" around points in which infinitesimals might reside. Perhaps aspects of logic break down, as they seem to in quantum mechanics, when dealing with microcosmic worlds. Rules for combining reals and non-traditional reals include: (A) the sum of two infinitesimals is infinitesimal, as is the product; (B) the product of a finite real number and an infinitesimal is an infinitesimal; (C) the product of an infinitesimal and an infinite number may be finite or infinite, depending upon the numbers involved, etc. We can also write a ≈ b ("a approximates b") if a-b is an infinitesimal. Hence, an infinitesimal ε ≈ 0. Let us call this new expanded real number system, *R. A function in *R is a set (finite or infinite) of ordered pairs of numbers such that no two pairs have the same 1st element, but different 2nd elements. Note that in *R, we might have, e.g., F = {(1,7), (3,π), (ε,∞), (ε+1,∞)}. Assuming that x and a are in the domain of a bounded function G and that a is a standard real number, we can say that G is continuous at a provided G(a) ≈ G(x) whenever x ≈ a. The area under a positive, continuous curve, given by f(x) on the interval [a,b], can be defined as the infinite sum of areas of rectangles constructed by subdividing [a,b] into an infinite number of subintervals, each of which is of infinitesimal width, and height the value of f(x) for some x in that subinterval. This is similar to the definition of an integral given in a calculus course, except that the thin rectangles are now very thin indeed! Suppose f(x) is a real valued function defined on the interval (a,b), with a and b standard reals. Let ζ , a standard real, be in the interior of (a,b). Then the derivative of f(x) at x = ζ may be expressed as ( f(ζ+ε) - f(ζ) )/ε , for all infinitesimals ε. For example, let f(x) = x² . Then ( f(ζ+ε) - f(ζ) )/ε = ( (ζ+ε)² - ζ² )/ε = ( 2εζ + ε² )/ε = 2ζ + ε ≈ 2ζ. Consider the Dirac Delta Function, δ(x) , using *R. This "function" is not really a function at all, and it can be described as a distribution in standard analysis, or as a measure, but roughly speaking, 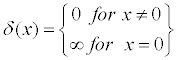 and
and
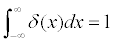
That is to say, the function is "so infinite" at x=0 that the "area" it encompasses above the x-axis is exactly 1.  This
is a "working function" used in physics and engineering, but it
clearly makes little sense in R, the standard reals. However,
there is a simple and playful heuristic
description in *R that is appealing:
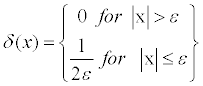 where ε
is some positive infinitesimal.
where ε
is some positive infinitesimal.The "area" under the
curve, above the x-axis, is (1/2ε)(2ε) = 1. Lots of luck, however, trying
to visualize this rectangle with infinitesimal width and infinite
height!
Abraham
(1966): ". . . we
observe that it [the
theory]
is presented naturally, within the framework of contemporary
mathematics, and thus appears to affirm the existence of all sorts of
infinitary entities. . . . it appears to us today that the infinitely
small and infinitely large numbers of a non-standard model of Analysis
are neither more nor less real than, for example, the standard
irrational numbers."
|