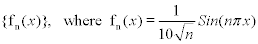 |
|
Is the Line Segment [0,1] Infinite? Consider the sequence of functions:
Each defined on
[0,1]. The
graphics above show functions with n = 2, n = 10, and n =
100.
It is easy to prove that the sequence converges uniformly to
the
straight line segment [0,1]. It is also straightforward to
demonstrate that the length of each curve is
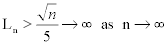 At any fixed degree of magnification, there is an n so large that the nth curve appears as a straight line. (Mathematicians routinely dismiss this sort of seeming paradox by simply citing "length" as a feature that is not preserved under uniform convergence.) Note, that for each n the maximum distance of the curve from the line segment [0,1] is 1/10√n . So for any positive real number r there is an n such that 0 < 1/10√n < r . As we pass from the finite to the infinite, entering the strange world of *R, the resulting object is an infinite line of no thickness - trapped in the interval [0,1] and having a "cloud" of infinitesimal points cloaking it, above and below.
|
|
A
very old example related to the one given above, one that confounded
mathematicians at the beginning of the 20th century - until they
decided to ignore it - is the Diagonal
Paradox :
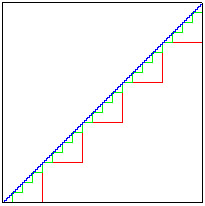 The
large square is one unit on a side. The "stairsteps" going from the
bottom left corner to the top right corner contain n=5, n=20, and n=110
steps, respectively. The length of each such staircase curve is exactly
2 units. But as n becomes infinite, the polygonal curves approach a
straight line: the diagonal of the large square, which is the square
root of 2 (approximately 1.414) units long. Again, as we pass
from the finite to the infinite, the result is a diagonal line of no
thickness, 2 units long, trapped within an interval 1.414 units long,
and sheathed in a halo of infinitesimal points.
Vardi Ilan (Paris) has an interesting comment about this kind of paradox: "Regarding the notion of finite curves of infinite length, I have |