www.johngill.net
| Mathematicae Varietas |
5
Power Series Functions analytic
in a neighborhood of z = 0, can be expanded as power series (Taylor's
Series) there:
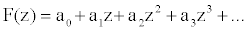 , ,
with radius of convergence
n = 10 and Image radius 4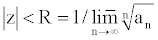 .
.Within the circle of convergence, the series converges uniformly to F(z), and outside the circle, it diverges. The convergence behavior on the circumference of the circle varies with the function. The following graphics show the regions of convergence of several functions, and how well the truncated series match the various functions, with darker hues indicating best approximations, and light hues, either divergence or poorer approximations. Example 1
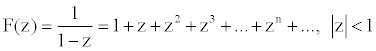
Example 2
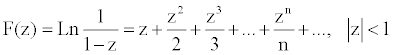
n = 50
Center of Image: 1+0i Image radius 1
Dark points are anomalies slightly outside circle of convergence, showing better approximations than expected. Example 3
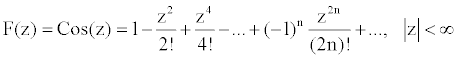
n = 5 (Polynomial of
degree 10) Image Radius 30
Red spots indicate better approximations than usual for that radius - blue shows poorer approximations
n = 10
(Polynomial of degree 20) Image Radius
30
|



