www.johngill.net
| Mathematicae Varietas |
6
Continued Fractions - Analytic Theory Continued Fractions
are algebraic constructions of the form
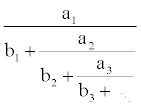 If this process does
not
terminate, the CF is said to be infinite, in the same way a
non-terminating series is said to be infinite. If the a(n)s
and
b(n)s are functions of a complex variable, z , and ω
is another such variable, we have
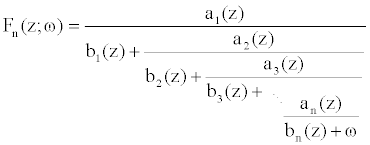 Called the normal
nth convergent of the infinite
CF when ω
= 0. Simpler notational formats include the
following:
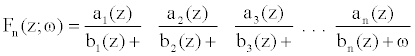 It is possible to expand complex functions as continued fractions using a number of distinct algorithms. This variety of expansion formats, plus a bewildering assortment of convergence theorems, contrasts strongly with the relative simplicity of power series expansions and their convergence criteria. Why then bother with CFs? Two reasons: (1) frequently CF expansions converge more rapidly than the series (although not always), and, (2) CF expansions may be valid in a much larger domain than power series. As a simple - even trivial - example, 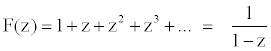 The series on the
left converges
in a disc about the origin of radius 1. It diverges outside this disc.
The expression on the right is, in fact, a finite CF, converging
instantly for all values of z with the exception of
z = 1.
We begin with
graphics, looking at a convergent of the periodic
CF,
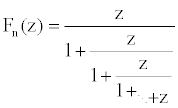 Going down to the nth level. This convergent is a rational function of degree n, having both fixed points and poles. Here we see how the nth convergent displaces points in the z-plane, with little or no displacement = dark and high displacement = light:
The
point z = 0 is,
of course, a
fixed point ( F(z) = z ). The graph of the 50th convergent shows a
series
of alternating poles and
what appear to be fixed points along the negative real axis (a portion
of which is actually the branch line for the single valued function of
which this is a CF expansion). The image
is centered at z = 0 and extends 2 units to the
right and
left.
Next, we expand the
function F(z) = p.v. √z
, about z = 0, obtaining another periodic CF:
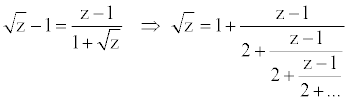 Comparing
graphically
the 10th
convergent with the value of the function F(z), we have
the following,
where darkest hues indicate strong approximations (<10^-5), and
light hues, poor approximations:
The
graph is centered
at the origin, extending 10 units to the right and left. The branch
line of the function extends from the origin along the negative real
axis. Poles of the rational approximation appear faintly as light spots
along the branch line.
|

