www.johngill.net
| Mathematicae Varietas |
7
Analytic Theory of Continued Fractions As an example of expansion into a CF of an analytic function, consider: F(z) = Arctan(z) .
From Continued Fractions: Analytic Theory and Applications, by W. Jones and W. Thron (1980), we have the following (written using a common format for CFs): 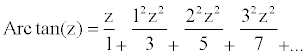 Valid
nearly everywhere in the
complex plane as the single-valued branch of the analytic function with
branch points at z = i and z = -i, and branch lines north
of i , and south of -i . To compute π/4 = arctan (1) to seven decimal places requires merely going out to the 9th convergent of the CF. Whereas, using the standard power series expansion:
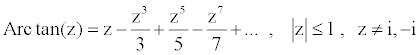 Valid only within the unit disc, one needs to employ (approximately) the first 500,000 terms of the series. Thus this example demonstrates the two previously stated reasons for using Cfs as functional expansions: greater speed of convergence and enhanced region of convergence.
The
speed of convergence of the CF expansion of Arctan(z), showing results
for the 15th convergent vs the 30th convergent. Graph is centered at
the origin, extending 10 units right and left ; branch lines above z =
i and below z = -i are clearly shown. The convergent
is, of course, a rational function approximation to the Arctangent, and
poles are illuminated along the branch lines. Dark areas indicate rapid
convergence of the CF.
A CF expansion of the function F(z) = - Ln( 1 - z ) ,
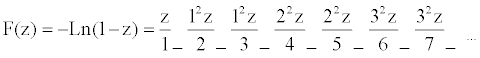 , ,converges and represents a
single-valued branch of the function in the complex plane, with branch
cut along the real axis to the right of z = 1. The speed
of convergence is displayed in the following graphic, where we compare
the 10th convergent to the 30th. As usual, dark = rapid, light = slow.
Since any convergent is merely a rational approximation to the
function, poles are seen illuminated along the branch cut. The scope of
the figure is |x|, |y| < 10.
As
we have seen before, the power series expansion of this function
about z = 0 fails to even converge outside of the unit disc.
|

